[0] GLAS-PPE/98-0327th June 1998
HERA Progress: Since last year's DIS workshop, the data available for analysis at ZEUS has more than doubled, corresponding to an integrated luminosity from the 1994-97 data-taking periods of 46.6 pb-1. This large data sample presents a significant challenge to the experimentalists in providing precise data in the many areas which HERA can uniquely access. The understanding of the ZEUS detector is being improved using the large data samples to calibrate in situ. To illustrate the current level of understanding of the detector: the integrated luminosity is currently known to better than ±1.5%; the overall momentum scale of the central tracking detector has been established at below the 0.3% level following calibration using elastic J/y data; the electron energy scale in the barrel calorimeter has been calibrated to ±1% using DIS data; and, the hadronic energy scale has been determined within ±3% using DIS data and cross-checked using dijet events. Developments in the calibration of the detector, combined with the improved statistics, enable increasingly precise as well as new measurements to be performed, as discussed below.
Photon Structure: [1] Before discussing the latest preliminary measurements, it is worthwhile to note the uncertainties, as discussed in recently published results on inclusive jet production using the cone algorithm. [2] Experimentally the uncertainty on the jet energy scale of ±3% dominates the uncertainty on the cross-sections. Theoretically, the scale dependence on the renormalisation and factorisation scales varied between ETjet/4 < mF = mR < ETjet, is minimised for a cone radius R ~ 0.6, as observed earlier at the Tevatron. The variation of Rsep, the two-jet merging parameter, leads to similar uncertainties on the cross-section for R < Rsep < 2R. In order to minimise the theoretical uncertainties due to merging/seed-finding ambiguities, the iterative kT-algorithm has been adopted. An inclusive dijet analysis was performed requiring ETjet1 > 14 GeV and ETjet2 > 11 GeV.

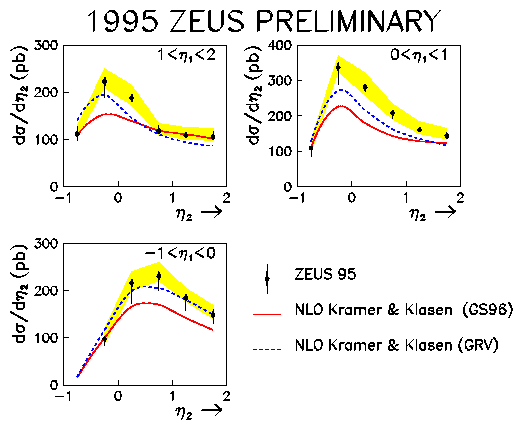
At these ETjet values, comparisons with Monte Carlo indicate that multiple interactions (not included in the NLO calculations) are not required to describe the observed xg distributions or the jet profiles. To gain greater sensitivity to the internal structure of the photon the measurements are made at high-y (0.5 < y < 0.85), corresponding to the highest accessible photon energies. In Fig. 1 the ds/dh2 distribution for the second-highest energy jet is presented for fixed intervals of h1. The shaded band represents the hadronic energy scale uncertainty. The hadronisation uncertainties have been estimated to be ~ 10%, the scale uncertainties are estimated at ~ 10% while the proton parton densities are well constrained in the probed x region (x ~ 10-2). The data are thus sensitive to the choice of photon parton densities, as illustrated by the comparison of the the data with the GS96 and GRV parameterisations. The ZEUS data has now reached a level of precision where the photon parton densities can be discriminated: a global analysis of photon parton densities incorporating such data is therefore required.
Multijet Structure: [3] In order to probe the QCD matrix elements at a deeper level, an inclusive three-jet analysis has been performed using the kT-algorithm for jets with ETjet > 6 GeV. The cross-section for such processes can be written as:
|
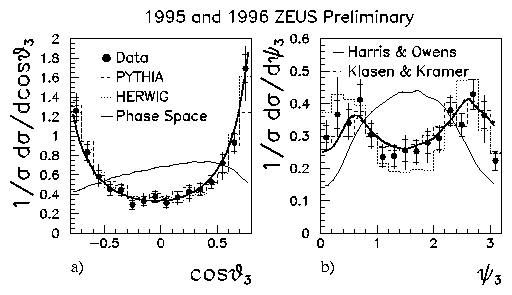
Here, the measured invariant mass distribution, M\sf jjj, is governed by the photon and proton parton densities, f\sf 1/\sf g(x\sf g) and f\sf 2/\sf p(x\sf p), whereas the scaled energies of the jets, X3 and X4, are controlled largely by phase space. The measured angular distributions in the three-jet centre of mass are cosq3, where q3 is the angle the highest-energy jet makes w.r.t. the beam axis, and y3, the angle of the three-jet plane w.r.t. the beam axis. The cosq3 distribution is determined by the spin of the primary exchange and the distribution of y3 is related to the coherence property of the radiated (lowest-energy) jet to lie in the plane of the beam and the highest-energy jet. These are shown in Fig. 2, compared to O(aaS2) calculations (thick line) as well as to a phase space calculation (thin line) where the spin of the partons is ignored. The comparisons constitute a refined test of the photoproduction QCD matrix elements M\sf 12® \sf 345.
Charm in Photoproduction: [4] Heavy flavour production introduces a new scale with which to test perturbative QCD. Measurements of the D*® (K p) ps and D*® (K ppp) ps channels are shown to be in good agreement in Fig. 3(a).
Two approaches have been taken in the calculations: the ``massive" approach (dashed lines) where charm is generated dynamically and divergences are regulated by the charm mass; and the ``massless" approach (full lines) where charm production is activated at the mc threshold and massless approximations are used. Uncertainties arise due to the choice of the effective charm mass, and renormalisation and factorisation scales (here mR = Ö{mc2 + p^2} = mF/2) as well as the hardness of the charm decay to D*, characterised in terms of ec in the Peterson fragmentation function for the ``massive" calculations. The measured cross-section is typically underestimated in the calculations. In Fig. 3(b) this excess is observed to be predominantly in the forward direction. The open question is whether the data are more sensitive to the choice of input photon structure function or to the D* fragmentation dynamics as we approach the proton fragmentation region or, perhaps, anomalously large contributions from b® c decays.
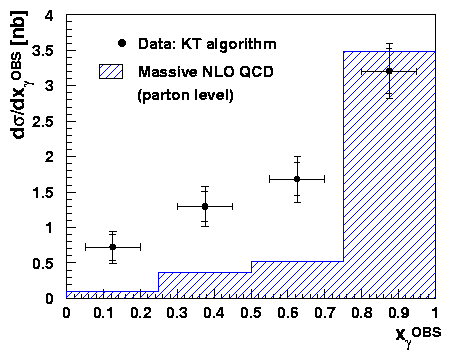
Further information is provided by the measurement of associated dijets with ETjet1 > 7 GeV and ETjet2 > 6 GeV shown in Fig. 4. Here the measurement of xgOBS has a relatively large contribution at low-xg whereas the ``massive" NLO calculation is significantly more peaked towards one, underestimating the low-xg part of the cross-section. The question here is whether the dynamical generation of charm in photoproduction is sufficient, assuming that jet hadronisation effects, estimated at ~ 10% using Monte Carlo simulations, are relatively less important.
Charm in DIS: [5]
D*® (K p) ps measurements in DIS provide a
significant test of the gluon density of the proton
determined from the scaling violations of F2.
They will also help to constrain theoretical uncertainties in the
fits to F2 where different prescriptions for heavy flavour effects
are adopted.
Compared to the photoproduction case, they remove the uncertainty
due to the choice of photon PDFs
and hence reduce the number of open question posed above.
The preliminary cross-section
sep® D*X = 8.55 ±0.40 +0.30-0.24 nb
is measured in the range
1 < Q2 < 600 GeV2,
0.02 < y < 0.7,1.5 < pT(D*) < 15 GeV, and h(D*) < 1.5.
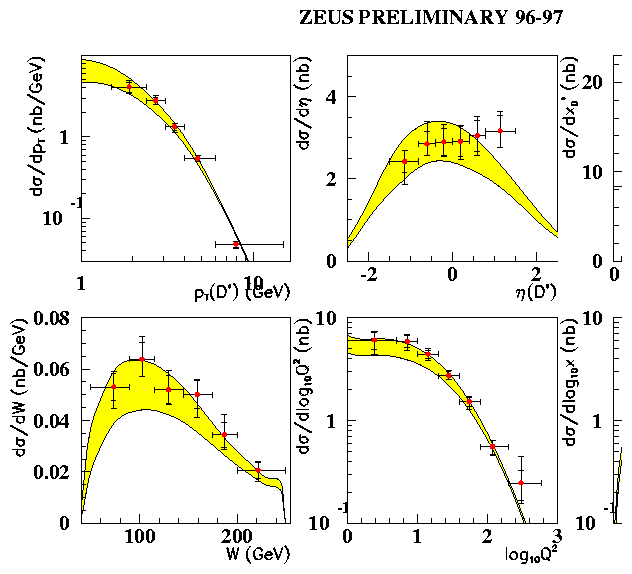
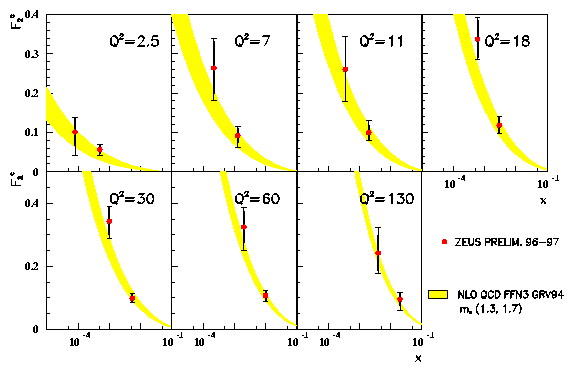
In Fig. 5, the upper plots show the measurements
of the hadronic final state variables pT(D*), h(D*) and xD*,
the fractional momentum the D* in the g* p rest frame:
the data agree with the massive NLO calculations where
ec = 0.035, except perhaps at lower
xD* corresponding to higher h(D*).
In addition the kinematic variables, W, Q2 and x shown in the
lower plots are in good agreement with the NLO calculations:
it is therefore reasonable to extrapolate the measured cross-section
to the full {h(D*), pT(D*) } range
2
to determine F2c(x, Q2) via the expression
|
Transition Region: [6] The corresponding rise of F2 with decreasing x, or equivalently the rise of stotg* p with increasing W, has stimulated significant theoretical developments in the understanding of QCD at high energies. One challenge is to explore how and where the transition occurs from soft to hard physics and interpret low-Q2 data. In order to relate the low-Q2 and Q2 = 0 data, a GVMD (Generalised Vector Meson Dominance) analysis has been performed. This analysis relates the virtual photon cross-section to the real cross-section via
stotg* p = stotgp·M20 / (M20 + Q2),
for fixed W (sL contributions at small Q2
lead to a small correction of stot).
A good description of the ZEUS BPC data measured in the range
0.1 < Q2 < 0.65 GeV2 is found with
M20 = 0.53 ±0.04 ±0.10 GeV2.
Extrapolating to Q2 = 0 GeV2, the corresponding
W2(\alphapom(0)-1) dependence
is given by the pomeron intercept value
\alphapom(0)BPC = 1.145 ± 0.02(stat) ± 0.04(sys) (preliminary)
to be compared with the Donnachie-Landshoff value \alphapom(0) = 1.08. In this Q2 range, the rise of the cross-section is therefore relatively modest. This behaviour is also seen in the lower Q2 points of Fig. 7(a). Here additional datsets are incorporated in fits to the F2 data of the form F2 = c·xleff |Q2. The parameter leff @ \alphapom(0) - 1 for x < 0.01 is then plotted as a function of Q2. A relatively slow transition from leff @ 0.1 is observed with increasing Q2. This rise of F2 with decreasing x is intimately coupled to the scaling violations via the gluon density (in leading order dF2/dlog Q2 ~ xg(x) neglecting sea quark contributions). In Fig. 7(b), fits of the form F2 = a + b ·log(Q2)|x have been performed to the published HERA data and the pre-HERA prediction from the GRV94 PDFs. [7] For x \lsim 10-4, corresponding to < Q2 > \lsim 2 GeV2 there is a qualitative change in behaviour where the scaling violations stabilise and then decrease for lower-x values, a behaviour which is not reproduced by the GRV94 PDFs. [r]60mm
file=sg_mor.ps Low Q2 parton densities.
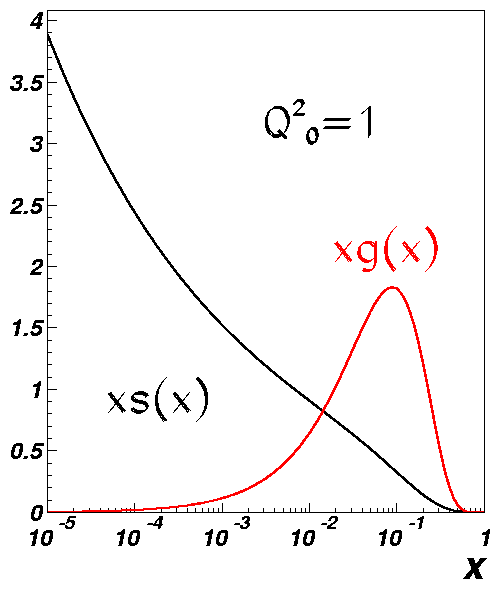
The question is whether this scaling violation behaviour and the slow onset of the rise of F2 with decreasing x can be simultaneously understood. A DGLAP NLO fit to the Q2 > 1 GeV2 data (not shown) describes the data, demonstrating that there is sufficient flexibility in such an approach to go down to relatively low Q2. However, the relatively stable scaling violations observed around < Q2 > ~ 2 GeV2 in Fig. 7(b) yield a gluon contribution which is rapidly diminishing at small-x and which is significantly smaller than the sea quark contribution for small starting scales, as illustrated in Fig. 8: in this low Q2 region the sea appears to be driving the gluon at low-x. For larger Q2 values the gluon dominates the sea and we have an intuitively appealing picture where gluons radiate sea quarks. Whether such low-Q2 partons are universally valid could be tested using e.g. low-Q2 F2c data.
Forward Jet Production: [8] Why does F2 rise? In the DGLAP approach the x dependence is an input determined at a starting scale Qo2 and evolved in Q2. In the BFKL approach the x-dependence has recently been calculated in NLO. The underlying dynamics may be tested using semi-inclusive forward jet measurements in low-x events. Jets with ET2 ~ Q2 and xjet \gsim x, where xjet is the momentum fraction of the jet relative to the incoming proton, are selected in order to enhance BFKL-like contributions where forward gluons may be emitted at relatively large ET. In Fig. 9 the jets observed at detector level are shown as a function of ET2/Q2 compared to three Monte Carlo simulations: LEPTO 6.5 and HERWIG 5.9 are DGLAP-based models such that gluons emitted at successively larger xgluon ~ xjet have successively lower ET whereas the colour dipole model ARIADNE 4.08 incorporates a BFKL feature that gluons are not strongly ordered.
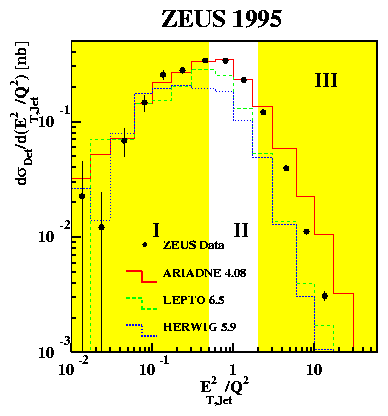
Three regions are identified: I - ET2 < Q2/2, the "DGLAP" region, where all models approximately describe the data; II - Q2/2 < ET2 < 2Q2, the "BFKL" region where the DGLAP-based models (LEPTO 6.5 and HERWIG 5.9) fall below the data; and, III - ET2 > 2Q2, where all models fail and we may need to describe the DIS data in terms of a virtual photon whose structure is being resolved by the high-ET jets. The cross-section is evaluated in region II as a function of x for xjet > 0.036 and ET > 5 GeV in Fig. 10. BFKL dynamics leads to an enhancement of the forward jet production cross-section proportional to (xjet/x)\alphapom -1 over the O(aaS2) calculation.
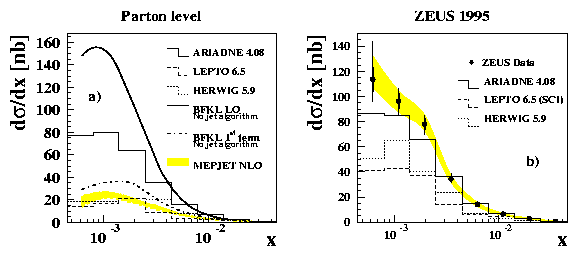
As shown in Fig. 10(a) there is a significant difference between the O(aaS2) MEPJET calculation (represented by the shaded band which includes the uncertainty on the renormalisation scale) compared to the leading-order BFKL prediction (full curve) at parton level. There are residual uncertainties in determining the hadron-to-parton level corrections and therefore the measurement in Fig. 10(b) is presented at hadron level. The rise of F2 at small x is mirrored by the rise of the measured forward jet cross-section which is not described by the DGLAP-based models. A consistent description of the F2 and forward-jet data represents a considerable challenge to our understanding of QCD.
Fragmentation Functions: Recently published results on jet shapes have shown that the observed patterns of QCD radiation in high-Q2 neutral current and charged current are similar to those observed in e+e- experiments. [9]
At HERA we are able to study these properties as a function of Q2 in a single experiment and hence provide detailed information on quark fragmentation properties. [10] These properties can be studied in the semi-soft limit by measuring the ln(1/xp) distributions, where xp = 2p/Q is the scaled momentum of charged hadrons in the current region of the Breit frame. The observed Gaussian distributions are then fitted within ±1 of the mean to yield the ln(1/xp)max values as a function of Q given in Fig. 11(a). The precise data are consistent with data from e+e- experiments establishing the universality of fragmentation over a large range of Q. An MLLA+LPHD fit (indicated by the full line) of the form ln(1/xp)max = 1/2Y +c2Ö(Y)-c22, where Y = lnQ/2Leff and c2 = 0.52 for three active flavours in the cascading process, provides a reasonable description of the data with Leff @ 245 MeV. The high-statistics data enables the region of high xp to be studied. In Fig. 11(b) the fragmentation function data are presented for different xp intervals as a function of Q2 (in various ranges of x). At high xp and higher Q2 the fragmentation functions exhibit negative scaling violations, consistent with a dominant QCD Compton process (c.f. high-x structure function data). The DIS data (full symbols) are observed to be reasonably consistent with e+e- data (open symbols), but systematically lower at intermediate xp values. Comparisons with NLO calculations where fragmentation functions extracted from e+e- data are implemented can describe the DIS data (see Fig. 2 in [10]). However care needs to be taken to explicitly include strange-quark fragmentation functions which are systematically softer than those of the up/down quarks. This is important since the production of strange quarks from the proton sea in DIS is suppressed (by a factor @ 0.2) compared to those from e+e- annihilation. In order to compare with recent 1/Q2 power-correction calculations, the fragmentation function data were also presented as function of x|| = 2 p·q /Q2 = 2pZ/Q, where the Z direction is defined by the virtual-photon proton axis.
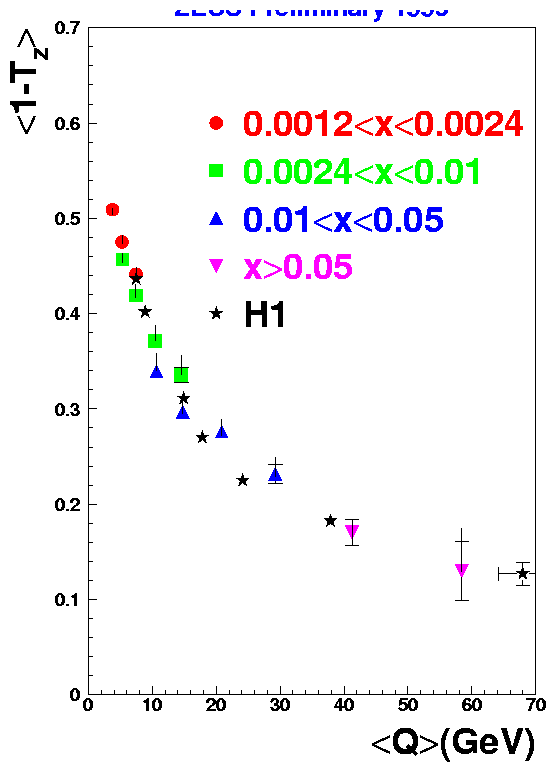
Another approach to investigate the rôle of such power corrections is to sum over these momenta and measure the corresponding thrust distributions TZ = 2 SpZ/ Sp. A series of event shape variables have been measured in the current region of the Breit frame where the power corrections, determined from renormalon calculations, are expected to be characterised by a universal [`(ao)] and to fall as 1/Q. In Fig. 12 the measurements using charged tracks in the current region of the Breit frame are displayed as < 1-TZ > versus Q. [11] The characteristic behaviour is in reasonable agreement with published H1 results given at slightly different x values. Other event shape variables are chosen which are relatively insensitive, in varying degrees, to soft gluon emission and collinear parton branchings in order to determine whether a universal [`(ao)] can be applied. As a first step, comparisons with NLO calculations illustrate the need for additional power correction terms (see Fig. 2 in [11]).
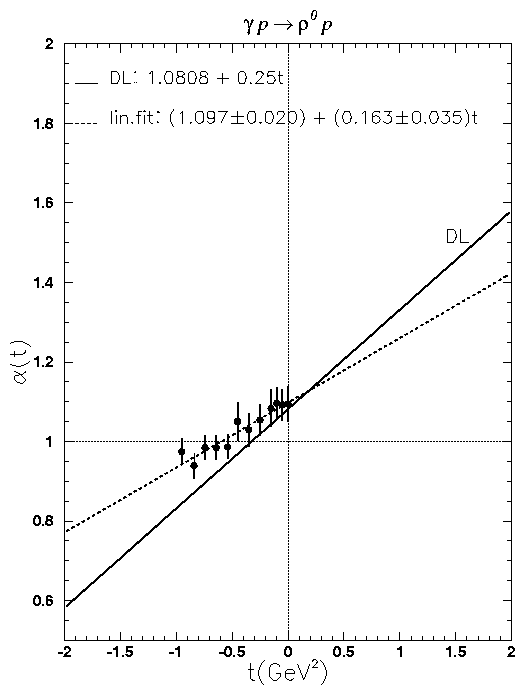
Vector meson t dependences: [13]
Diffraction is characterised
by a steeply-falling dependence
of the cross-section as a function of t,
the momentum transferred at the proton vertex.
This characteristic fall-off increases approximately linearly
with increasing W.
This ``shrinkage"
behaviour is built into the Donnachie-Landshoff pomeron
a(t)r0 = (1.097±0.020) + (0.163±0.035)·t (preliminary)
a(t)J/y = (1.175±0.026) + (-0.015±0.065)·t (preliminary).
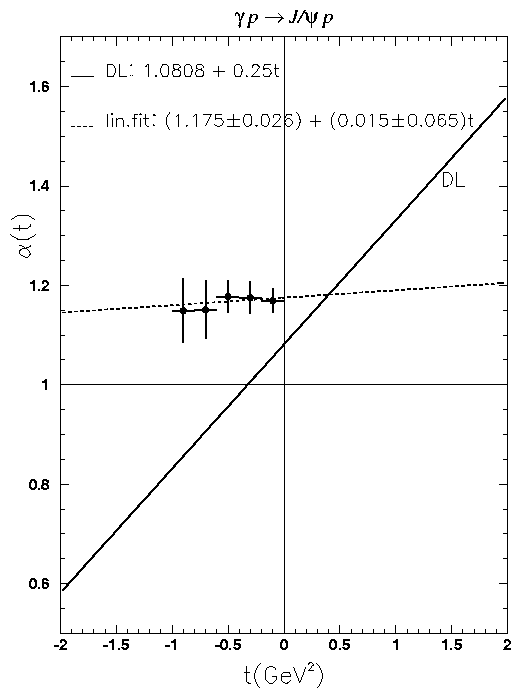
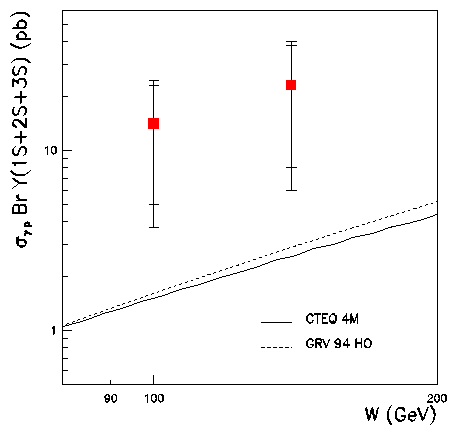
Higher Mass Vector Mesons: [14] Twenty years after the discovery of the U, the first observation of a signal in photoproduction is shown in Fig. 14(a) as a broad enhancement around 10 GeV in the di-muon mass spectrum. The insert in Fig. 14(a) indicates the J/y and y¢ resonances: the y¢/y production ratio is measured to be R = 0.16 ±0.02 ±0.04, where the largest contribution to the systematic uncertainty is on the y¢® m+m- branching ratio. The result is in agreement with QCD calculations, determined by the wavefunction at the origin for the 1S and 2S states, of @ 0.17. The observation of the U leads to the measurement of the elastic cross-section for the unresolved U(1S), U(2S) and U(3S) states shown in Fig. 14(b). Here the relative rates or muon production from the U states is determined from CDF data and applied as a correction to the U(1S) calculation. Comparison with the leading-order QCD calculations, where sdiff ~ xg(x)2 Ä[^(s)] , indicates that the measured cross-section is above these expectations.
Diffractive Structure Functions: [15] A new era for diffraction was opened by the observation of large rapidity gap events in DIS and their subsequent analysis in terms of a diffractive cross-section. The diffractive contribution is identified as a non-exponentially suppressed contribution at small masses, MX, of the dissociating virtual photon system. In Fig. 15 the ratio of this diffractive contribution to the total virtual photon proton cross-section is given as a function of W for various MX intervals.
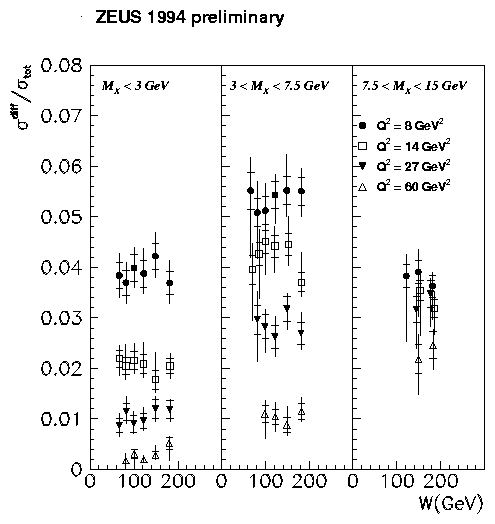
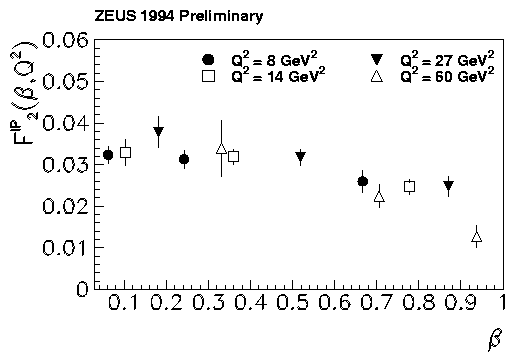
An approximately constant ratio with W indicates a diffractive contribution which rises with a similar W dependence. This simple observation is contrary to the näive expectation where the diffractive contribution is identified with the forward part of the scattering amplitude and would therefore rise twice as quickly as the total cross-section as a function of W. The rise of the diffractive cross-section with W can be parameterised in terms of a power law, yielding \alphapom(0) = 1.16 ±0.01 ±0.02 (preliminary), after integration over t with a mean exponential slope, b = 7 GeV-2 and assuming a¢ = 0.25 GeV-2. In order to understand the driving mechanism responsible for this rise, the cross-sections at fixed MX and W are plotted in terms of scaling variables. Integrating over \xpom, the momentum fraction of the pomeron within the proton, leads to the b dependence of F2D(2) (b,Q2) ( º F2\pom specified at \xpom = 0.0042) shown in Fig. 16 where b is the momentum fraction of the struck quark within the pomeron. An approximately flat dependence on b is observed and an approximate scaling in Q2 emerges from analysis of the data. The decreasing fraction of events in each MX interval with increasing Q2 observed in Fig. 15 can thus be seen as due to integrating over a decreasing b @ Q2/(Q2+MX2) region which is approximately flat in b.
Diffractive Event Shapes: [17] The measurements of the structure function of the pomeron constrain various models of diffraction. These models may be discriminated using event shape variables which are directly sensitive to the underlying partonic structure. Similarly, the data can be directly compared with e+e- data where the underlying gluon Bremsstrahlung structure is well known. Tagging a leading proton in the LPS allows a wide range of MX up to 25 GeV to be explored for \xpom < 0.03 and Q2 > 4 GeV2.
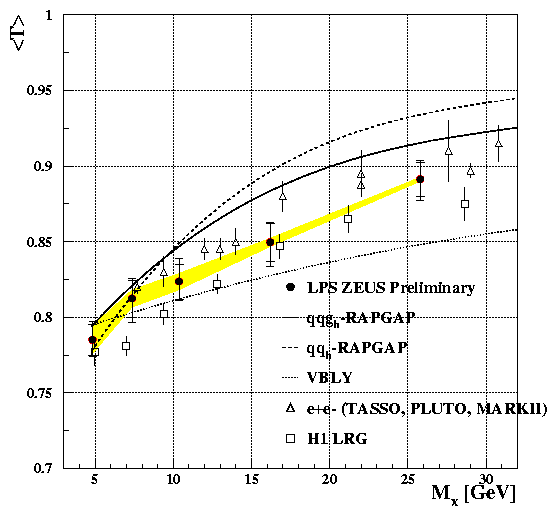
Measurements of the mean thrust are presented as a function of MX in Fig. 17. The LPS measurements are able to discriminate amongst various models which assign different partonic structures to the pomeron. The data exhibit reasonably similar values compared to e+e- data for all values of MX suggesting that additional gluon contributions from the pomeron are relatively small. They are also consistent, but systematically higher than, the H1 data obtained using the large rapidity gap method. Improved statistics, from existing data, will help to clarify whether the gluon contribution of the pomeron determined from the scaling violations of F2D(2) [15] is consistent with that extracted from event shape variables [17] and diffractive dijet photoproduction [16].
Leading Baryon Production: [18] Non-diffractive contributions play a rôle at higher values of \xpom. Measurements of forward proton production allow us to compare data with fragmentation models as well as models based on reggeon exchange. Preliminary results for the corrected rates of proton production in the range 0.60 < xL º 1-\xpom < 0.91 for DIS at low and higher Q2 (0.1 < Q2 < 0.8 GeV2 and Q2 > 4 GeV2) are (13.0±0.5+0.7-0.8)% and (12.7±0.3±0.9)%, respectively. The measured rates are typically higher than the currently available fragmentation models by a factor of 1.5 to 2. Measurements of uncorrected forward neutron production rates have been compared to reggeon exchange models: the comparisons indicate that the internal structure of the exchanged reggeon falls like 1-b at large b (a dependence similar to p (and higher) Regge exchanges), in contrast to the approximately flat behaviour with b noted earlier for diffractive exchange. The rates for neutron production are approximately the same for DIS, photoproduction and even proton-gas interactions although the W dependence of these cross-sections is significantly different. This suggests that ``diquark" fragmentation is a universal process which is to a large extent independent of the type of interaction with the incident proton.
In Fig. 18(a), these events clearly stand out but no new NC outstanding events are observed in the 1997 data, corresponding to a further 26.5 pb-1 of data. In Fig. 18(b), one charged current (CC) event is observed at very high Q2 @ 30,000 GeV2 from the 1994-1996 data as well as two further events from 1997 at Q2 @ 20,000 GeV2. The number of events is higher than expectations but is consistent with the standard model. Attention has therefore focussed on measuring the cross-sections at the highest accessible Q2 values. The theoretical uncertainty on the cross-sections was determined from a ZEUS QCD fit to the structure function data on proton and deuteron targets from SLAC, BCDMS and NMC as well as the neutrino measurements from CCFR, taking into account the correlation amongst the systematic errors of each experiment. aS(M2Z) was varied from 0.113 to 0.123 and a 50% uncertainty in the strange quark content was included. In addition, various published PDFs with different models for charm evolution were used as well as fits incorporating E706 prompt photon data and CDF jet data. The results yielded SM cross-section uncertainties of @ 6-8% on the NC cross-section and @ 6-12% on the CC cross-section at the highest accessible Q2 values. These cross-sections therefore represent a benchmark for the standard model. The cross-sections, discussed below, are corrected to the electroweak Born level and integrated over the complete y range.
Charged Current Cross-Sections: [19] Charged current events are identified by their missing transverse momentum (pT) due to the escaping neutrino. The cross-section is sensitive to the valence d-quark distribution in the proton:
|
MW = 78.6 + 2.5- 2.4(stat.) +3.3- 3.0(syst.) GeV (preliminary)
Photoproduction of W-bosons decaying semi-leptonically has been investigated by searching for events with a high-pT lepton and missing pT with 46.6 pb-1 of data. This is interesting in the context of the observed excess of high-pT muons with associated missing pT observed by H1 [20]. In the ZEUS analysis four events are observed in the electron channel where 2.22±0.02 are expected from W production and 1.24±0.35 from various backgrounds. Similarly, zero events are observed in the muon channel where 0.46±0.02 are expected from W production and 0.84±0.23 from other sources. The ZEUS measurements enable 95%CL limits to be set on s(W) (pTmiss > 20 GeV) of 2.5 pb and 2.0 pb in the electron and muon channels, respectively.
Neutral Current Cross-Sections: [21] High-Q2 neutral current events are easily identified from the high-energy scattered positron. The cross-section is particularly sensitive to the valence u-quark distribution in the proton:
|
A wide range of new interactions would modify the NC cross-sections in a way which can be parameterised by an effective four-fermion (eq® eq) coupling. Given a convention for the strength of the coupling (g2 = 4p), limits can be placed on the effective mass scale (L) of these contact interactions. Scalar and tensor terms are constrained by earlier experiments and atomic parity violation experiments provide strong constraints on various vector couplings: the relative size and sign of individual terms in the contact interaction amplitudes is therefore limited to 24 different combinations. These contact interactions all contain a term proportional to 1/L4 which enhances the cross-section as well as a SM interference term proportional to 1/L2 which can either enhance or suppress the cross-section at intermediate Q2. No significant deviations are found and limits on the 24 models are set in the range of L @ 2-5 TeV. These limits are competitive with, and in some cases extend, those limits set from from hadronic cross-section measurements at LEP and Drell-Yan electron pair production at the Tevatron.
1 Alexander von Humboldt fellow (Hamburg II University), supported by DESY and PPARC.
2 This procedure neglects the possibility of additional contributions outside the measured region due, for example, to intrinsic charm.