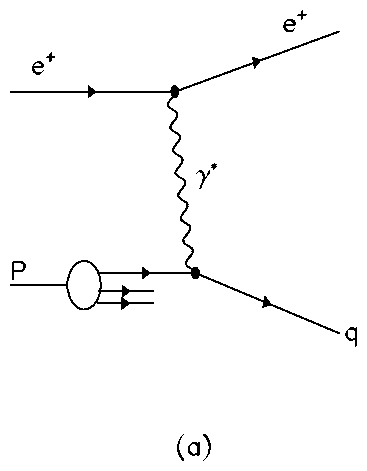
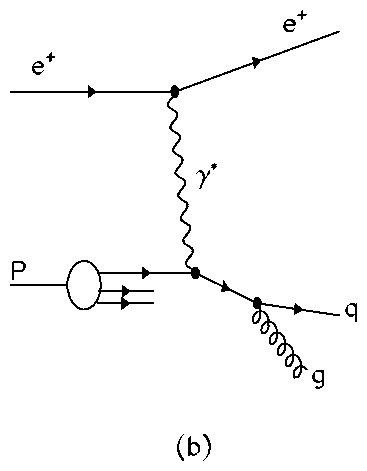
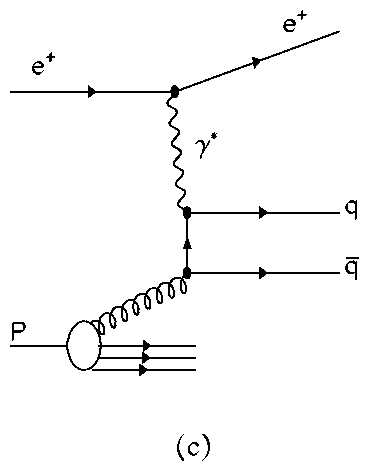
Neutral current (NC) DIS occurs when an uncharged boson (g, Z0) is exchanged between the lepton and proton. In QPM there is a 1+1 parton configuration, fig. 1a, which consists of a single struck quark and the proton remnant, denoted by ``+1''. At HERA energies there are significant higher-order quantum chromodynamic (QCD) corrections: to leading order in the strong coupling constant, as, these are QCD-Compton scattering (QCDC), where a gluon is radiated by the scattered quark and boson-gluon-fusion (BGF), where the virtual boson and a gluon fuse to form a quark-antiquark pair. Both processes have 2+1 partons in the final state, as shown in fig. 1. There also exists calculations for the higher, next-to-leading (NLO) processes.
HERA provides a unique opportunity to study the scale behaviour of Quantum Chrmodynamics in a single experiment with a cleaner background environment than that obtainable at hadron colliders. The data presented here were taken in 1994 and onwards at the ep collider HERA using the H1 and ZEUS detectors. During this period HERA operated with positrons of energy Ee = 27.5 GeV and protons with energy 820 GeV. A detailed descriptions of the H1 and ZEUS detectors can be found in refs. [2] and [3] respectively.
At small x the dominant parton is the gluon and the description of the structure function is driven by the behaviour of the gluon. Because of gluon splitting, g ® q[`q], pQCD suggests the small x behaviour of the sea quark and gluon distributions are strongly correlated.
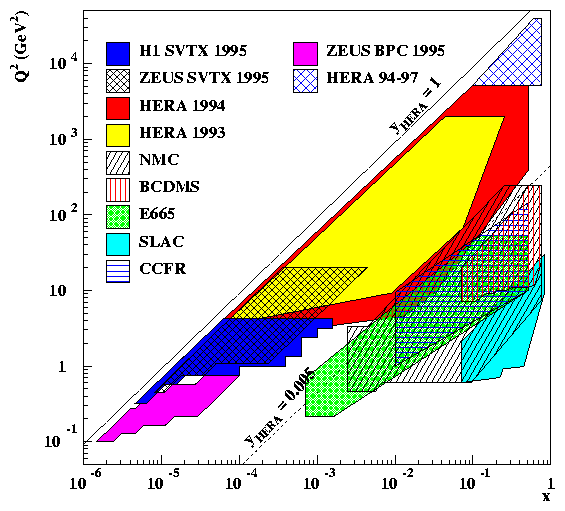
The kinematic plane covered by HERA and the fixed target measurements is shown in fig. 3. HERA has increased the reach in Q2 by about 2 orders of magnitude and can also probe nearly 3 orders of magnitude further down in x. The low x region is correlated with low values of Q2. The differential NC DIS cross section is related to three structure functions:
| (1) |
where Y± = 1 ±(1-y)2. The structure function F2 in QPM is just the sum of the quark densities multiplied by the appropriate electric charge; F3 arises from the weak part of the cross section and is negligible for Q2 < 5000 GeV2, and FL is the longitudinal structure function and only becomes important for y > 0.6. Hence by measuring the differential cross section at HERA one is effectively measuring the structure function F2.
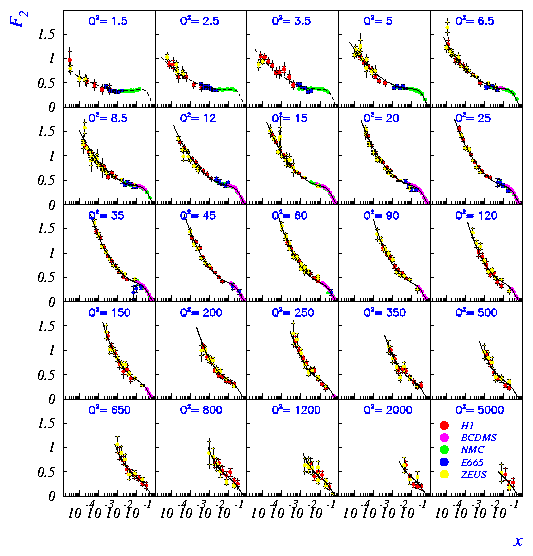
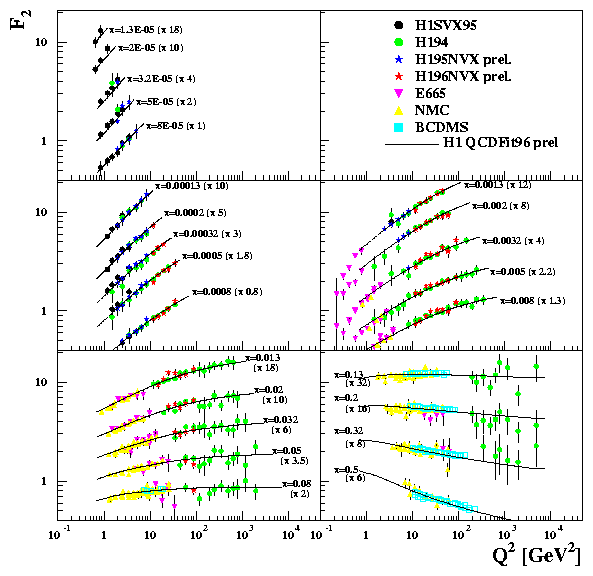
The F2 measurements are shown in figs. 4 and 5 as a function of x and Q2 respectively. The error bars are at the 5-10% level and the normalisation uncertainty is ~ 2%. There is a steep rise of F2 with decreasing x in all Q2 bins, fig. 4. Scaling violations in Q2 are clearly seen in fig. 5. Both H1 and ZEUS have performed next to leading order (NLO) QCD fits [6,7] based on the DGLAP evolution equations using both HERA and fixed target data. Fig. 5 shows that these QCD fits describe the F2 data well, though it should be noted that the data can also be satisfactorily described by the BFKL prediction [8].
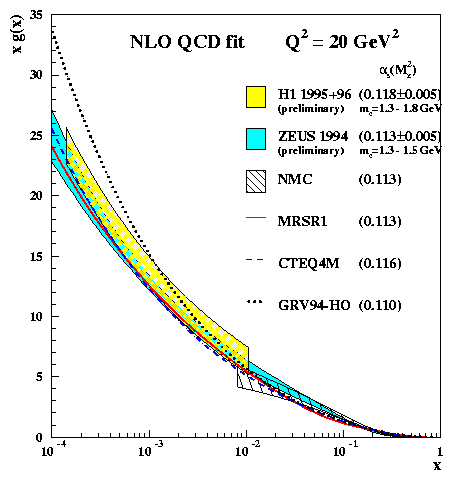
The scaling violations from the HERA data allow an estimate of the gluon density xg(x) at low values of x, whilst the fixed target data are used to constrain the high x region. The extracted gluon densities from the fits are shown in fig 6 for a fixed Q2 = 20 GeV2. The error band shows the statistical and systematic uncertainty taking into account correlations and variations in the mass of the charm quark, mc, and the strong coupling constant, as. The results of the two HERA experiments are in good agreement and the extracted densities agree with the results of NMC [9] for large x. The resulting gluon distributions show a clear rise with decreasing x and have a 15% uncertainty at x ~ 5×10-4. These NLO QCD fits are also in good agreement with the global QCD analyses performed by MRS [10] and CTEQ [11], whilst the prediction from the dynamical evolution of GRV [12] is too steep for x < 10-3.
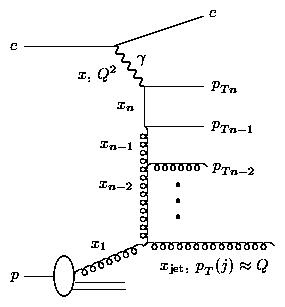
In Fig. 7, recent data from H1 [13] and ZEUS [14] are compared with BFKL predictions [16] and fixed order QCD predictions as calculated with the MEPJET [15] program at NLO. The conditions pT(j) @ Q and xjet >> x are satisfied in the two experiments by slightly different selection cuts. H1 selects events with a forward jet of pT(j) > 3.5 GeV (in the angular region 7o < q(j) < 20o) with
| (2) |
| (3) |
Fig. 7 shows that both experiments observe a forward jet cross section which rises steeply with decreasing x with substantially more forward jet events than expected from NLO QCD (labelled as Born in fig. 7a.) A BFKL calculation (the stars) gives a better agreement with the data. The overall normalisation in this calculation is uncertain and the agreement may be fortuitous. Indeed, it should also be noted that both experiments observe more centrally produced dijet events than predicted by the NLO QCD calculations. The ARIADNE Monte Carlo (CDM) model describes the steeply increasing jet cross section with decreasing x. The ARIADNE model does not have a strong ordering in transverse momentum in the QCD cascade, akin to BFKL type dynamics, although it does not make explicit use of the BFKL equation. Whilst those models that adhere to the DGLAP formalism (LEPTO and HERWIG) fail to predict this large growth. Further careful investigation is necessary before claiming that BFKL is the mechanism for this enhanced forward jet production.
A natural frame in which to study the dynamics of the hadronic final state in DIS is the Breit frame [19]. In this frame the exchanged virtual boson is purely space-like with 3-momentum q = (0,0,-Q), the incident quark carries momentum Q/2 in the positive Z direction, and the outgoing struck quark carries Q/2 in the negative Z direction. A final state particle has a 4-momentum pB in this frame, and is assigned to the current region if pBZ is negative, and to the target frame if pBZ is positive. The advantage of this frame lies in the maximal separation of the outgoing parton from radiation associated with the incoming parton and the proton remnant, thus providing the optimal environment for the study of the fragmentation of the outgoing parton.
In e+e- annihilation the two quarks are produced with equal and opposite momenta, ±Ös/2. This can be compared with a quark struck from within the proton with outgoing momentum -Q/2 in the Breit frame. In the direction of the struck quark (the current fragmentation region) the particle momentum spectra, xp = 2pB/Q, are expected to have a dependence on Q similar to those observed in e+e- annihilation [20,21,22] at energy Ös = Q.
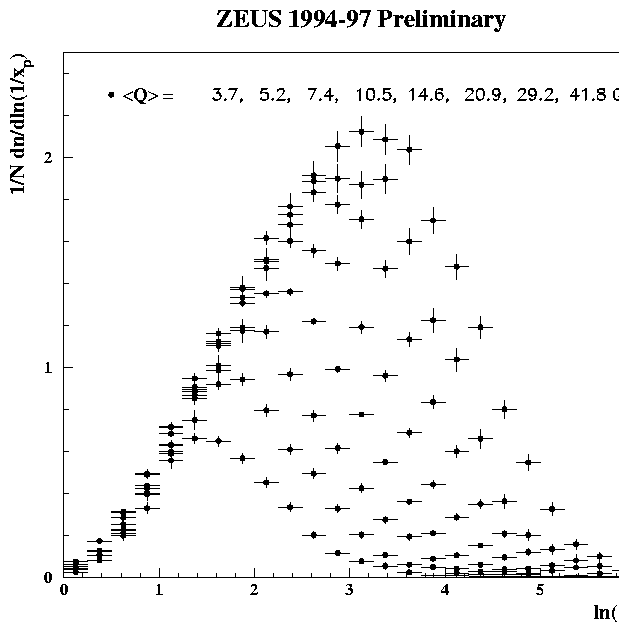
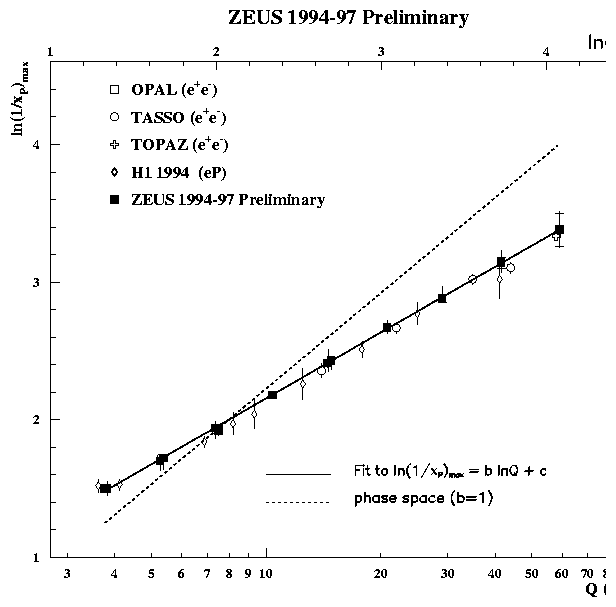
In fig 8 the log(1/xp) distributions for charged particles in the current fragmentation region of the Breit frame are shown as a function of Q2. These distributions are approximately Gaussian in shape with mean charged multiplicity given by the integral of the distributions. As Q2 increases the multiplicity increases and the the peak of the distributions shifts to larger values of log(1/xp). Figure 9 shows this peak position, log(1/xp)max, as a function of Q for the HERA data and of Ös for the e+e- data. Over the range shown the peak moves from @ 1.5 to 3.3. The HERA data points are consistent with those from TASSO and TOPAZ and a clear agreement in the rate of growth of the HERA points with the e+e- data at higher Q is observed.
The increase of log(1/xp)max can be approximated phenomenologically by the straight line fit log(1/xp)max = b log(Q)+c also shown in figure 9. The values obtained from the fit to the ZEUS data are b = 0.69 ±0.01(stat) ±0.03(sys) and c = 0.56 ±0.02 +0.08-0.09. The gradient extracted from the OPAL and TASSO data is b = 0.653±0.012 (with c = 0.653±0.047) which is consistent with the ZEUS result. This value is consistent with that published by OPAL, b = 0.637±0.016, where the peak position was extracted using an alternative method [23]. A consistent value of the gradient is therefore determined in DIS and e+e- annihilation experiments.
Also shown is the statistical fit to the data when b = 1 (c = 0.054 ±0.012) which would be the case if the QCD cascade was of an incoherent nature, dominated by cylindrical phase space. The observed gradient is clearly inconsistent with b = 1 and therefore inconsistent with cylindrical phase space.
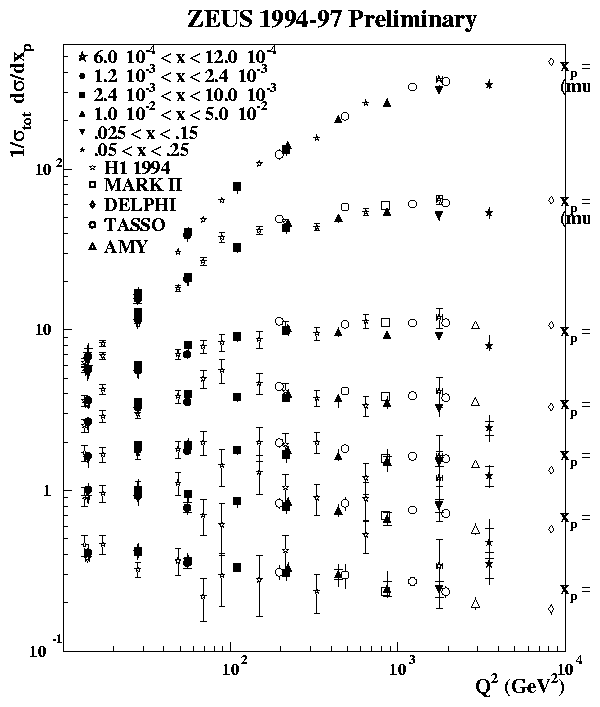
The inclusive charged particle distribution, 1/stot ds/dxp, in the current fragmentation region of the Breit frame are shown in bins of xp and Q2 in fig. 10. The increasingly steep fall-off, at fixed Q2, towards higher values of xp as Q2 increases, shown in figure 10, corresponds to the production of more particles with a smaller fractional momentum, and is indicative of scaling violation in the fragmentation function. For Q2 > 80 GeV2 the distributions rise with Q2 at low xp and fall-off at high xp and high Q2. In figure 10 the HERA data are compared at Q2 = s to e+e- data [25], again divided by two to account for the production of both a q and [`q]. In the Q2 range shown there is good agreement between the current region of the Breit frame in DIS and the e+e- experiments.
The intriguing rise of F2 at small x can be well described using conventional DGLAP evolution equations. The data though can also be described by the BFKL approach thus giving rise to ambiguities how to treat QCD in this small x regime. In order to resolve these ambiguities jet production in the forward direction has been studied and the cross section for such jets is seen not to be reproduced by Monte Carlo models based on DGLAP parton shower evolution.