


Next: Exclusive Production of Vector
Up: Diffraction: QCD Effects in
Previous: Diffraction: QCD Effects in
Prologue:
In 1992, H. Fritzsch summarised the status of
``QCD 20 Years On" [1]
with the words
``A very large amount of data in strong-interaction physics is described by
the pomeron singularity...
The fact that the physics of the pomeron is very simple needs to be
explained in equally simple terms in QCD...
Using HERA the experimentalists will be able to study the region of very
low x in deep inelastic scattering... Furthermore, both in
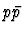 -scattering at high energies and at HERA the structure functions of
the pomeron can be studied in more detail."
Now, 25 years on from the first developments of QCD,
at the 25th SLAC Summer Institute we can discuss
a series of diffractive measurements that have been made in the
intervening period at HERA and the Tevatron.
-scattering at high energies and at HERA the structure functions of
the pomeron can be studied in more detail."
Now, 25 years on from the first developments of QCD,
at the 25th SLAC Summer Institute we can discuss
a series of diffractive measurements that have been made in the
intervening period at HERA and the Tevatron.
HERA Kinematics:
The diffractive processes studied at HERA are of the form:
where the photon dissociates into the system X and the outgoing
proton, p', remains intact, corresponding to single dissociation,
as illustrated in Fig. 1.
The measurements are made as a function of the photon virtuality,
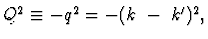 the centre-of-mass energy of the virtual-photon proton system,
W2=(q + P)2,
the invariant mass of the dissociated system, X, denoted by M2
and the four-momentum transfer at the proton vertex, given by
t = (P - P')2.
the centre-of-mass energy of the virtual-photon proton system,
W2=(q + P)2,
the invariant mass of the dissociated system, X, denoted by M2
and the four-momentum transfer at the proton vertex, given by
t = (P - P')2.
Figure 1:
Kinematic variables of diffractive ep scattering
at HERA
![\begin{figure}
\epsfxsize=8.cm
\centering
\leavevmode
\epsfbox[110 270 480 570]{diagr_diff.ps}\end{figure}](img40.gif) |
Signatures of diffraction:
The processes studied build upon the basic elastic scattering process
which is constrained through the measurement of the
corresponding total cross-section
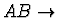 anything,
via the optical theorem.
The diffractive processes measured are then
anything,
via the optical theorem.
The diffractive processes measured are then
where the systems X and Y have a limited mass compared to the
overall energy available, W. The process is thought of as being mediated
by the exchange of an object with vacuum quantum numbers
(in particular, no colour is exchanged in the process).
A signature for diffraction is via the momentum
fraction carried by the exchanged colour singlet state.
When this fraction is less than 1% of the momentum of, say,
particle B (in the infinite momentum frame of B) we
can interpret this as being largely due to pomeron exchange.
The kinematics of producing two low-mass outgoing states
(X and B or X and Y)
with a small momentum fraction exchanged between them
therefore leads to a rapidity gap.
The high energy available at HERA provides a large rapidity span,
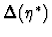 ,
of
,
of 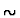 12 units
(here,
12 units
(here,
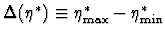 where
where
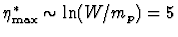 and
and
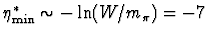 for a typical
for a typical
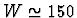 GeV).
A colour singlet exchange of reggeons (dominating at lower W)
and the pomeron (dominating at higher W) can be used to interpret the
data on single dissociation and double dissociation reactions.
Fluctuations from processes where colour is
exchanged may also generate low-mass states. However, these will be
exponentially suppressed: the (Poisson) probability of not
producing a given particle in the rapidity gap
GeV).
A colour singlet exchange of reggeons (dominating at lower W)
and the pomeron (dominating at higher W) can be used to interpret the
data on single dissociation and double dissociation reactions.
Fluctuations from processes where colour is
exchanged may also generate low-mass states. However, these will be
exponentially suppressed: the (Poisson) probability of not
producing a given particle in the rapidity gap
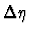 when the
two systems are colour connected is
when the
two systems are colour connected is
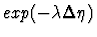 ,
where
,
where
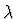 is the mean particle density for a given
is the mean particle density for a given
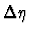 interval.
This exponential fall-off reflects the plateau in the
corresponding (non-diffractive) multiplicity distribution as a function
of
interval.
This exponential fall-off reflects the plateau in the
corresponding (non-diffractive) multiplicity distribution as a function
of 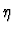 which increases relatively slowly (logarithmically) with
increasing W [2].
which increases relatively slowly (logarithmically) with
increasing W [2].
In Fig. 2, the t distributions of pp elastic scattering
data are illustrated as a function of the longitudinal momentum (pL)
of the outgoing proton transformed to a fixed-target rest frame.
The patterns
are similar to the diffraction patterns observed when light is scattered
from an aperture and exhibit an exponential fall-off for values of t
below  1 GeV2.
This characteristic fall-off
increases with increasing energy, a property known as shrinkage, and
differs for different incident
and outgoing systems. In order to characterise the t-dependence, a fit to
the diffractive peak is performed.
In the most straightforward approach,
a single exponential fit to the t distribution,
1 GeV2.
This characteristic fall-off
increases with increasing energy, a property known as shrinkage, and
differs for different incident
and outgoing systems. In order to characterise the t-dependence, a fit to
the diffractive peak is performed.
In the most straightforward approach,
a single exponential fit to the t distribution,
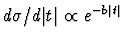 for
for
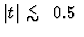 GeV2 is adopted.
Physically, the slope of the t dependence in diffractive interactions
tells us about the effective radius of that interaction, RI:
if d
GeV2 is adopted.
Physically, the slope of the t dependence in diffractive interactions
tells us about the effective radius of that interaction, RI:
if d
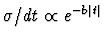 ,
then
,
then 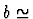 RI2/4.
RI2/4.
Figure:
Signatures of diffraction:
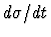 for ISR pp data as a function of pL,
the longitudinal momentum of the outgoing proton transformed to
a fixed-target rest frame, from 24 GeV
(uppermost plot) to 1496 GeV (lowest plot).
for ISR pp data as a function of pL,
the longitudinal momentum of the outgoing proton transformed to
a fixed-target rest frame, from 24 GeV
(uppermost plot) to 1496 GeV (lowest plot).
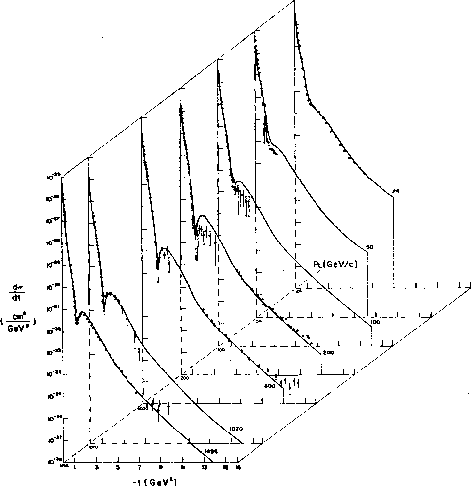 |
Regge trajectories:
The subject of diffraction is far from new: diffractive processes
have been measured and studied for more than thirty years [3].
Their relationship to the corresponding total cross-sections at high energies
has been successfully interpreted via the optical theorem and Regge theory.
At lower energies the colour singlet exchange of virtual mesons,
called reggeons, contribute to the fall of the cross-section with increasing
energy. At higher energies,
the introduction of an additional
trajectory, known as the pomeron trajectory,
with a characteristic W2 and t dependence is
necessary [4].
The energy behaviour of the total cross-sections can then be described by the
sum of two power-law dependences on the centre-of-mass energy,
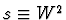
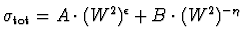 |
|
|
(1) |
where W is measured in GeV,
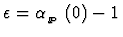 and
and 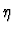 is defined to be positive
such that
is defined to be positive
such that
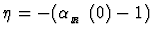 .
Here,
.
Here,
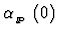 and
and
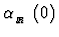 are the pomeron and reggeon intercepts
(i.e. the values of the parameters at t = 0 GeV2),
respectively.
A wide range of total cross-section data
are used to determine the parameters
are the pomeron and reggeon intercepts
(i.e. the values of the parameters at t = 0 GeV2),
respectively.
A wide range of total cross-section data
are used to determine the parameters 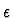 and
and 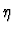 .
The fall-off at low energy due to reggeon exchange
constrains the value of
.
The fall-off at low energy due to reggeon exchange
constrains the value of
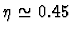 .
The slow rise of hadron-hadron total cross-sections with increasing
energy indicates that the value of
.
The slow rise of hadron-hadron total cross-sections with increasing
energy indicates that the value of
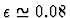 i.e. the total
cross-sections increase as W0.16, although the
i.e. the total
cross-sections increase as W0.16, although the 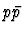 data from CDF at two
data from CDF at two 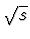 values indicate
values indicate
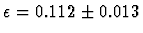 [5].
Recent fits using all pp and
[5].
Recent fits using all pp and 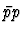 data are consistent with a value
of
data are consistent with a value
of
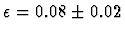 which will be used here to characterise this
behaviour [6].
which will be used here to characterise this
behaviour [6].
Figure:
Regge trajectories:
The degenerate regge trajectories are indicated by the solid line.
The pomeron trajectory is indicated by the dashed line.
Also indicated are the 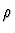 ,
,
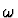 ,
f and a resonances as well as
the
I(JPC) = 0(2++) glueball candidate state X(1900) observed by
the WA91 collaboration [7].
,
f and a resonances as well as
the
I(JPC) = 0(2++) glueball candidate state X(1900) observed by
the WA91 collaboration [7].
![\begin{figure}
\epsfxsize=8.cm
\centering
\leavevmode
\epsfbox[28 407 300 650]{traj.ps}\end{figure}](img73.gif) |
In a Regge analysis, the diffractive data
are interpreted via exchanges with spin
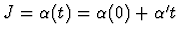 and
and
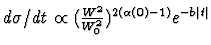 ,
with
,
with
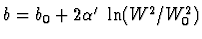 .
At lower energies, these correspond to reggeon
(i.e. approximately degenerate
.
At lower energies, these correspond to reggeon
(i.e. approximately degenerate 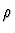 ,
,
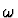 ,
f and a) exchanges.
At the highest energies, where the pomeron contribution dominates,
the optical theorem relates the total cross-sections
to the elastic, and hence diffractive, scattering amplitude at the same W2.
In Fig. 3, the trajectories,
,
f and a) exchanges.
At the highest energies, where the pomeron contribution dominates,
the optical theorem relates the total cross-sections
to the elastic, and hence diffractive, scattering amplitude at the same W2.
In Fig. 3, the trajectories,
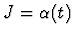 ,
are shown as a function
of M2.
The diffractive data probe the region of negative t.
Given the dominance of the
pomeron contribution at large W
and an approximately exponential behaviour of the
|t| distribution with slope b, whose mean
,
are shown as a function
of M2.
The diffractive data probe the region of negative t.
Given the dominance of the
pomeron contribution at large W
and an approximately exponential behaviour of the
|t| distribution with slope b, whose mean 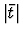 value
is given by 1/b at the mean
value
is given by 1/b at the mean 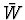 of a given data sample,
the diffractive cross-section
rise is moderated from
of a given data sample,
the diffractive cross-section
rise is moderated from
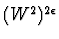 to
to
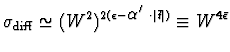 |
|
|
(2) |
where
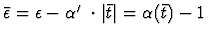 and
and
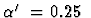 GeV-2 reflects the shrinkage of the
diffractive peak as a function of t with increasing W2.
The observed shrinkage of the diffractive peak
therefore corresponds to a relative reduction
of the diffractive cross-section with increasing energy.
This value may be compared with the corresponding parameter
GeV-2 reflects the shrinkage of the
diffractive peak as a function of t with increasing W2.
The observed shrinkage of the diffractive peak
therefore corresponds to a relative reduction
of the diffractive cross-section with increasing energy.
This value may be compared with the corresponding parameter
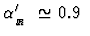 GeV-2 for reggeon exchanges.
GeV-2 for reggeon exchanges.
Maps of the Pomeron:
Whilst these Regge-based models gave a unified description of
pre-HERA diffractive data, this approach is not fundamentally linked
to the underlying theory of QCD.
It was anticipated that at HERA and Tevatron energies
if any of the scales Q2, M2 or t become larger than the
QCD scale 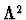 ,
then
it may be possible to apply perturbative QCD (pQCD) techniques, which
predict changes to this power law behaviour.
Qualitatively, the W dependence could be ascribed
to the rise of the gluon density with decreasing x
determined from the large scaling violations of
F2(x,Q2),
where x is the Bjorken scaling variable,
,
then
it may be possible to apply perturbative QCD (pQCD) techniques, which
predict changes to this power law behaviour.
Qualitatively, the W dependence could be ascribed
to the rise of the gluon density with decreasing x
determined from the large scaling violations of
F2(x,Q2),
where x is the Bjorken scaling variable,
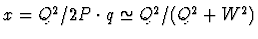 .
QCD factorisation into a long-timescale and short-timescale process,
where this timescale is characterised by 1/Q or 1/M or
.
QCD factorisation into a long-timescale and short-timescale process,
where this timescale is characterised by 1/Q or 1/M or
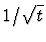 ,
leads to the following approaches.
,
leads to the following approaches.
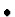
- For exclusive final states, e.g. vector meson production, with a hard
scale the approach is very simple
i.e. two-gluon exchange where Gp2 is the square of
the gluon density of the proton at a representative value of x and
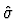 represents the hard scattering process.
The rise of F2 with decreasing x, which constrains the gluon density,
corresponds to an increase in the effective value of
represents the hard scattering process.
The rise of F2 with decreasing x, which constrains the gluon density,
corresponds to an increase in the effective value of 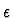 .
This brings us from the regime of dominance of the slowly-rising
``soft" pomeron to the newly emergent ``hard" behaviour and the question
of how a transition may occur between the two.
The QCD expectation is that the cross-sections should approximately scale as
a function of t, corresponding to a weak dependence of
.
This brings us from the regime of dominance of the slowly-rising
``soft" pomeron to the newly emergent ``hard" behaviour and the question
of how a transition may occur between the two.
The QCD expectation is that the cross-sections should approximately scale as
a function of t, corresponding to a weak dependence of 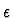 as a
function of t and therefore a decrease of
as a
function of t and therefore a decrease of
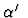 for the
perturbative pomeron.
for the
perturbative pomeron.
- For inclusive diffraction with a hard scale
i.e. leading-gluon exchange where Gp is the gluon density of
the proton,
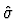 represents the hard scattering process and H represents
the hadronisation process. Here, the final state with a leading proton
is seen as a particular hadronisation process [8].
For processes involving one incoming hadron, the above
approaches can be tested and compared with experimental data.
represents the hard scattering process and H represents
the hadronisation process. Here, the final state with a leading proton
is seen as a particular hadronisation process [8].
For processes involving one incoming hadron, the above
approaches can be tested and compared with experimental data.
- Finally, one can break the process down further and invoke
Regge factorisation where a flux of pomerons,
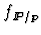 lead to partons from the pomeron,
lead to partons from the pomeron,
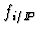 ,
which interact and
hadronise
,
which interact and
hadronise
For processes involving two incoming hadrons, this approach has been
generalised to
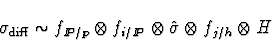
where fj/h represents the partons from the hadron which
has not diffractively dissociated. This Regge factorisation
approach can therefore be experimentally tested when diffractive data
from HERA and the Tevatron are compared.
Precisely where the Regge-based approach breaks down or
where pQCD may be applicable is open to experimental question.
In addition, once we observe ``hard" diffractive phenomena, we can
ask whether the pQCD techniques applied to inclusive processes
also apply to these exclusive colour singlet exchange reactions.
The emphasis is therefore on the internal (in)consistency of
a wide range of measurements of diffractive and total cross-sections.
As an experimentalist navigating around the various theoretical concepts of
the pomeron, it is sometimes difficult to see which direction to take
and what transitions occur where (Fig. 4(a)).
However, from an experimental perspective, the directions are clear,
even if the map is not yet complete (Fig. 4(b)).
Figure 4:
Maps of the pomeron:
(a) theoretical and (b) experimental directions.
![\begin{figure}
\vspace{1.0cm}
\epsfxsize=10cm
\centering
\leavevmode
\epsfbox[45 497 507 732]{maps_PICT.ps}\end{figure}](img98.gif) |
Outline:
The HERA collider allows us to observe a broad range of diffractive
phenomena at high W2.
What is new is that we have the ability to observe the variation
of these cross-sections at specific points on the M2
scale, from the  up to the
up to the  system as discussed in
section 2.
Similarly, the production cross-section can be explored
as a function of Q2, using a virtual photon probe.
The observation of a significant fraction of events (
system as discussed in
section 2.
Similarly, the production cross-section can be explored
as a function of Q2, using a virtual photon probe.
The observation of a significant fraction of events (
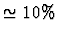 )
with a large rapidity gap
between the outgoing proton and the rest of the final state
in deep inelastic scattering (DIS)
has led to measurements of the internal structure of the pomeron.
In addition, the leading proton spectrometer
data, where the diffracted proton is directly measured, enable
the t distribution as well as the structure function to be determined
simultaneously. These results are discussed in section 3.
Studies of the hadronic final state in events with a large
rapidity gap, including transverse energy flows,
event shape distributions and high-pT jets,
have been used to provide complementary information on this
structure.
Also, the observation of rapidity gaps between jets, corresponding to
large-t diffraction, are presented in section 4.
Many of these hadronic final state investigations were initiated
at
)
with a large rapidity gap
between the outgoing proton and the rest of the final state
in deep inelastic scattering (DIS)
has led to measurements of the internal structure of the pomeron.
In addition, the leading proton spectrometer
data, where the diffracted proton is directly measured, enable
the t distribution as well as the structure function to be determined
simultaneously. These results are discussed in section 3.
Studies of the hadronic final state in events with a large
rapidity gap, including transverse energy flows,
event shape distributions and high-pT jets,
have been used to provide complementary information on this
structure.
Also, the observation of rapidity gaps between jets, corresponding to
large-t diffraction, are presented in section 4.
Many of these hadronic final state investigations were initiated
at 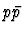 colliders. In section 5, the latest results from the
Tevatron on diffractive dijet and
colliders. In section 5, the latest results from the
Tevatron on diffractive dijet and 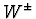 production, rapidity gaps
between jets and first observations of hard
double-pomeron exchange are presented.
A comparison of hard diffractive event rates at HERA and the Tevatron
is given and the interpretation of the observed differences is
discussed.
production, rapidity gaps
between jets and first observations of hard
double-pomeron exchange are presented.
A comparison of hard diffractive event rates at HERA and the Tevatron
is given and the interpretation of the observed differences is
discussed.



Next: Exclusive Production of Vector
Up: Diffraction: QCD Effects in
Previous: Diffraction: QCD Effects in
Converted by www person
1998-02-27
![]() 1 GeV2.
This characteristic fall-off
increases with increasing energy, a property known as shrinkage, and
differs for different incident
and outgoing systems. In order to characterise the t-dependence, a fit to
the diffractive peak is performed.
In the most straightforward approach,
a single exponential fit to the t distribution,
1 GeV2.
This characteristic fall-off
increases with increasing energy, a property known as shrinkage, and
differs for different incident
and outgoing systems. In order to characterise the t-dependence, a fit to
the diffractive peak is performed.
In the most straightforward approach,
a single exponential fit to the t distribution,
![]() for
for
![]() GeV2 is adopted.
Physically, the slope of the t dependence in diffractive interactions
tells us about the effective radius of that interaction, RI:
if d
GeV2 is adopted.
Physically, the slope of the t dependence in diffractive interactions
tells us about the effective radius of that interaction, RI:
if d
![]() ,
then
,
then ![]() RI2/4.
RI2/4.

![]()
![\begin{figure}
\epsfxsize=8.cm
\centering
\leavevmode
\epsfbox[28 407 300 650]{traj.ps}\end{figure}](img73.gif)
![]() and
and
![]() ,
with
,
with
![]() .
At lower energies, these correspond to reggeon
(i.e. approximately degenerate
.
At lower energies, these correspond to reggeon
(i.e. approximately degenerate ![]() ,
,
![]() ,
f and a) exchanges.
At the highest energies, where the pomeron contribution dominates,
the optical theorem relates the total cross-sections
to the elastic, and hence diffractive, scattering amplitude at the same W2.
In Fig. 3, the trajectories,
,
f and a) exchanges.
At the highest energies, where the pomeron contribution dominates,
the optical theorem relates the total cross-sections
to the elastic, and hence diffractive, scattering amplitude at the same W2.
In Fig. 3, the trajectories,
![]() ,
are shown as a function
of M2.
The diffractive data probe the region of negative t.
Given the dominance of the
pomeron contribution at large W
and an approximately exponential behaviour of the
|t| distribution with slope b, whose mean
,
are shown as a function
of M2.
The diffractive data probe the region of negative t.
Given the dominance of the
pomeron contribution at large W
and an approximately exponential behaviour of the
|t| distribution with slope b, whose mean ![]() value
is given by 1/b at the mean
value
is given by 1/b at the mean ![]() of a given data sample,
the diffractive cross-section
rise is moderated from
of a given data sample,
the diffractive cross-section
rise is moderated from
![]() to
to
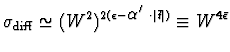
![]() ,
then
it may be possible to apply perturbative QCD (pQCD) techniques, which
predict changes to this power law behaviour.
Qualitatively, the W dependence could be ascribed
to the rise of the gluon density with decreasing x
determined from the large scaling violations of
F2(x,Q2),
where x is the Bjorken scaling variable,
,
then
it may be possible to apply perturbative QCD (pQCD) techniques, which
predict changes to this power law behaviour.
Qualitatively, the W dependence could be ascribed
to the rise of the gluon density with decreasing x
determined from the large scaling violations of
F2(x,Q2),
where x is the Bjorken scaling variable,
![]() .
QCD factorisation into a long-timescale and short-timescale process,
where this timescale is characterised by 1/Q or 1/M or
.
QCD factorisation into a long-timescale and short-timescale process,
where this timescale is characterised by 1/Q or 1/M or
![]() ,
leads to the following approaches.
,
leads to the following approaches.
![]() up to the
up to the ![]() system as discussed in
section 2.
Similarly, the production cross-section can be explored
as a function of Q2, using a virtual photon probe.
The observation of a significant fraction of events (
system as discussed in
section 2.
Similarly, the production cross-section can be explored
as a function of Q2, using a virtual photon probe.
The observation of a significant fraction of events (
![]() )
with a large rapidity gap
between the outgoing proton and the rest of the final state
in deep inelastic scattering (DIS)
has led to measurements of the internal structure of the pomeron.
In addition, the leading proton spectrometer
data, where the diffracted proton is directly measured, enable
the t distribution as well as the structure function to be determined
simultaneously. These results are discussed in section 3.
Studies of the hadronic final state in events with a large
rapidity gap, including transverse energy flows,
event shape distributions and high-pT jets,
have been used to provide complementary information on this
structure.
Also, the observation of rapidity gaps between jets, corresponding to
large-t diffraction, are presented in section 4.
Many of these hadronic final state investigations were initiated
at
)
with a large rapidity gap
between the outgoing proton and the rest of the final state
in deep inelastic scattering (DIS)
has led to measurements of the internal structure of the pomeron.
In addition, the leading proton spectrometer
data, where the diffracted proton is directly measured, enable
the t distribution as well as the structure function to be determined
simultaneously. These results are discussed in section 3.
Studies of the hadronic final state in events with a large
rapidity gap, including transverse energy flows,
event shape distributions and high-pT jets,
have been used to provide complementary information on this
structure.
Also, the observation of rapidity gaps between jets, corresponding to
large-t diffraction, are presented in section 4.
Many of these hadronic final state investigations were initiated
at ![]() colliders. In section 5, the latest results from the
Tevatron on diffractive dijet and
colliders. In section 5, the latest results from the
Tevatron on diffractive dijet and ![]() production, rapidity gaps
between jets and first observations of hard
double-pomeron exchange are presented.
A comparison of hard diffractive event rates at HERA and the Tevatron
is given and the interpretation of the observed differences is
discussed.
production, rapidity gaps
between jets and first observations of hard
double-pomeron exchange are presented.
A comparison of hard diffractive event rates at HERA and the Tevatron
is given and the interpretation of the observed differences is
discussed.